COM: core 2 summary

COM: Core 2 abstractions

ABS: Y

ABS: t.2

ABS: t.1

ABS: x(s)

ABS: x(s1,s2)

ABS: x(s1,s2,s3)

ABS: x(s1,s2,s3,s4)

ABS: x(s1,s2,s3,s4,s5)

ABS: x(a,b,c,d,e,f)

ABS: x(a,b,c,d,e,f,g)

ABS: x f y

ABS: 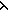x. t(x)

ABS: 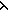x,y. t(x;y)

ABS: t  ...$L

ABS: {T}

ABS: ???

ABS: 

ABS: A c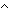 B

ABS: parm{i}

COM: CORE WF THEOREMS

STM: false wf

STM: true wf

STM: squash wf

STM: guard wf

STM: unit wf

STM: not wf

STM: comb for not wf

STM: rev implies wf

STM: comb for rev implies wf

STM: iff wf

STM: comb for iff wf

STM: nequal wf

STM: member wf

STM: comb for member wf

COM: COMBS acom

ABS: I

STM: icomb wf

ABS: K

STM: kcomb wf

ABS: S

STM: scomb wf

COM: PRODUCT DEFS acom

STM: pi1 wf

STM: pi2 wf

STM: pair eta rw

ABS: let x,y,z = a in t(x;y;z)

ABS: let w,x,y,z = a in t(w;x;y;z)

ABS: let a,b,c,d,e = u in v(a;b;c;d;e)

ABS: let a,b,c,d,e,f = u in v(a;b;c;d;e;f)

ABS: let a,b,c,d,e,f,g = u in  v(a;b;c;d;e;f;g)

COM: UNIT DEFS acom

ABS: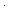 

STM: it wf

STM: unit triviality

COM: CONSTR PROPERTIES com

ABS: Dec(P)

STM: decidable wf

STM: decidable or

STM: decidable and

STM: decidable implies

STM: decidable false

STM: decidable not

STM: decidable iff

STM: decidable int equal

STM: decidable lt

STM: decidable le

STM: decidable atom equal

STM: iff preserves decidability

ABS: Stable{P}

STM: stable wf

STM: stable not

STM: stable function equal

STM: stable from decidable

ABS: SqStable(P)

STM: sq stable wf

STM: sq stable and

STM: sq stable implies

STM: sq stable iff

STM: sq stable all

STM: sq stable equal

STM: sq stable squash

STM: sq stable from stable

STM: sq stable not

STM: sq stable from decidable

ABS: XM

STM: xmiddle wf

STM: sq stable iff stable

STM: squash elim

COM: LOGIC THMS tcom

STM: dneg elim

STM: dneg elim a

STM: iff symmetry

STM: and assoc

STM: and comm

STM: or assoc

STM: or comm

STM: not over or

STM: not over or a

STM: not over and b

STM: not over and

STM: and false l

STM: and false r

STM: and true l

STM: and true r

STM: or false l

STM: or false r

STM: or true l

STM: or true r

STM: exists over and r

STM: not over exists

COM: EQUALITY THMS tcom

STM: equal symmetry

COM: REWRITE SUPPORT tcom

STM: iff transitivity

STM: implies transitivity

STM: and functionality wrt iff

STM: and functionality wrt implies

STM: implies functionality wrt iff

STM: implies functionality wrt implies

STM: decidable functionality

STM: iff functionality wrt iff

STM: all functionality wrt iff

STM: all functionality wrt implies

STM: exists functionality wrt iff

STM: exists functionality wrt implies

STM: not functionality wrt iff

STM: not functionality wrt implies

STM: or functionality wrt iff

STM: or functionality wrt implies

STM: squash functionality wrt implies

STM: squash functionality wrt iff

STM: implies antisymmetry

COM: GENERALIZATION tcom

STM: gen hyp tp

COM: MISC DEFS com

ABS: let x = a in b(x)

STM: let wf

COM: type inj acom

ABS: [x]{T}

COM: choicef com

ABS: 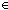x:T. P(x)

STM: choicef wf

STM: choicef lemma

STM: fun thru spread

STM: spread to pi12

ABS: {a:T}

STM: singleton wf

STM: singleton properties

ABS: {!x:T | P(x)}

STM: unique set wf

ABS: a = !x:T. Q(x)

STM: uni sat wf

STM: uni sat imp in uni set

STM: sq stable uni sat

STM: comb for pi1 wf

STM: comb for pi2 wf

COM: core 2 end